Binomische Formeln
Die Binomischen Formeln tauchen oft bei der Rechnung mit Potenzen auf. Sie Vereinfachen das Rechnen erheblich. Anstatt nämlich zwei große Zahlen multiplizieren zu müssen, brauchen die Schüler nach Anwendung der binomischen Formeln nur noch zwei kleinere Zahlen miteinander multiplizieren und deren Summe bilden.
Erste binomische Formel (Plus-Formel)
$(a+b)^2 = (a+b)(a+b) = a^2+2ab+b^2$
Zweite binomische Formel (Minus-Formel)
$(a-b)^2 = (a-b)(a-b) = a^2-2ab+b^2$
Dritte binomische Formel (Plus-Minus-Formel)
$(a+b)(a-b) = a^2+ba-ab-b^2 = a^2 - b^2$
Pascalsche Dreieck
Mit hilfe des Pascalschen Dreiecks lässt sich der Binomische Lehrsatz in N-Graden herleiten.
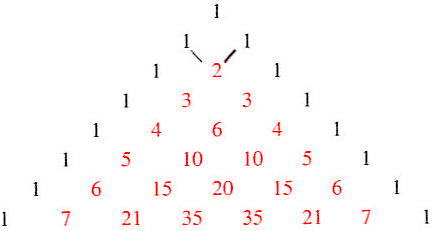
(Quelle: frustfrei-lernen.de)
Die Addition zweier benachbarter Zahlen bilden die darunterstehende Zahl.
$ (a+b)^2 = a^2+\color{red}{2}ab+b^2 \\ (a+b)^3 = a^3+\color{red}{3}a^2b+\color{red}{3}ab^2+b^3 \\ (a+b)^4 = a^4+\color{red}{4}a^3b+\color{red}{6}a^2b^2+\color{red}{4}ab^3+b^4 \\ (a+b)^5 = a^5+\color{red}{5}a^4b+\color{red}{10}a^3b^2+\color{red}{10}a^2b^3+\color{red}{5}ab^4+b^5 \\ (a+b)^6 = a^6+\color{red}{6}a^5b+\color{red}{15}a^4b^2+\color{red}{20}a^3b^3+\color{red}{15}a^2b^4+\color{red}{6}ab^5+b^6 \\ (a+b)^7 = a^7+\color{red}{7}a^6b+\color{red}{21}a^5b^2+\color{red}{35}a^4b^3+\color{red}{35}a^3b^4+\color{red}{21}a^2b^5+\color{red}{7}ab^6+b7 \\ $